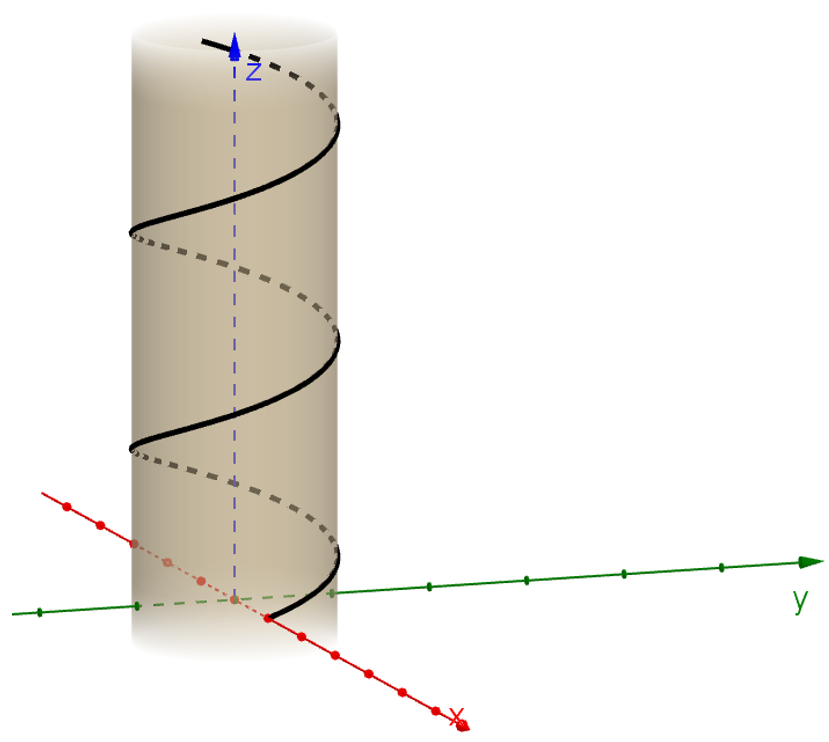
A cardboard kitchen roll tube is modelled as a cylinder of diameter \(5\) units and height \(23\) units.
A line which spirals around the tube is modelled as having parametric equations:
.\( x= \frac{5}{2} cos(t), y=\frac{5}{2}sin(t), z=\frac{23t}{5\pi} (0 \le t \le 5 \pi ). \)
If I cut along the line and flatten out the cardboard, what is the perimeter of this shape (to 4 sig.figs.)?
Please login to submit answer.

