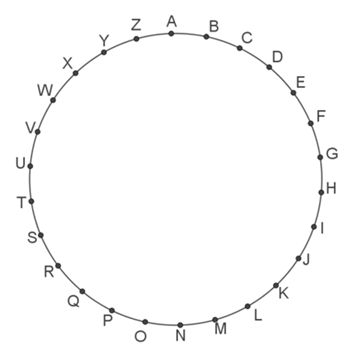
The 26 letters of the alphabet are equally spaced, in alphabetical order, around this circle.
The shortest route along the circle from R to I is 9 steps (anticlockwise).
The shortest route from I to T is 11 steps (clockwise).
To spell RITANGLE in this way, starting at the first letter and always using the shortest route between each pair of successive letters, requires 9+11+7+13+7+5+7=59 steps. Call this the path length of RITANGLE.
The path length of INTEGRAL is 55 steps (and every step is clockwise!)
Consider the path length for each of the 8! arrangements of the letters R-I-T-A-N-G-L-E.
If the shortest path length is \(x\) steps and the longest path length is \(y\) steps, what is \(x \times y\) ?
Please login to submit answer.
